前言

在使用上一篇讲述的傅里叶滤波作出一些结果后，王老师建议我换一下其他滤波方法试一下。我注意到文献中使用 Lanczos 和 Butterworth 滤波方法较多，所以打算研究一下这类滤波方法。

本文参考的文献有：

《Data Analysis Methods in Physical Oceanography, Third Edition》

《lanczos filtering in one and two dimensions》

《气候变率诊断和预测方法》

Lanczos 滤波

Lanczos滤波的本质是对时间长度为 $N$ 的原时间序列 $x(n)$ 的各个点进行加权，形成新的序列 $y(n)$。即

$$
\begin{equation}
{y_n} = \sum\limits_{k = - M}^M { {w_k} x_{n - k} } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} n = 0,1,…,N - 1
\end{equation}
$$

其中 $w_{k}$ 即是权重。$M$ 表征权重点的个数 ($2M+1$个)，它是根据需要自己定义的， $M$ 越大滤波的效果越好，但损失的数据越多。

  • 为什么会损失数据？

    公式 (1) 中 $n$ 最大是N-1, 最小是0。然而 $x$ 的小标为 $n-k$ 。当 $n=0, k=M$ 时，$ x_{n-k}=x_{-M} $ , 然而 $x$ 的索引不可能取到负数。因此 $n=0$ 这个点无法通过公式计算出新序列。同样的 $n=0,1,…M-1$ 和 $n=N-M,…,N-1$ 都无法通过公式计算得到新序列值。新序列会比原序列在左端少 $M$ 个，在右端少 $M$ 个，共少 $2M$ 个。(类似于5点滑动平均，左端和右端会各少2个点)。

    以上损失数据的情况在NCL的函数 filwgts_lanczos 体现出来。 然而，在我自己进行编程计算的时候发现，如果把原序列看做周期为其自身长度的周期信号，即 $x_{0} = x_{N}, x_{-1}=x_{N-1}$ （傅里叶变换中也用了相似的思想）。这样计算就不会产生数据损失，在序列两端的滤波结果仍具有很好的准确性 (将在下面的程序试验中验证)。

如果 $M=4, w_{k}=\frac{1}{2M+1}=\frac{1}{9}$, 那么公式 (1) 变为

$$
\begin{equation}
{y_n} = \frac{1}{9}\sum\limits_{k = - 4}^4 { {x_{n - k} } }
\end{equation}
$$

这就是九点滑动平均公式，它是一种低通滤波，过滤掉周期小于9年的信号。在这里权重被设为常数 $\frac{1}{9}$ 。一旦权重 $w_{k}$ 被确定下来，那么这个滤波也就完成了。因此Lanczos滤波就是要找到一个合适权重系数，至少要比九点滑动平均的权重系数要好。

高通/低通滤波

这个权重系数就是

  • 低通

    $$
    \begin{align}
    &{w_k} = \frac{ { {\omega _c} } } { { {\omega _N} } }\frac{ {\sin (\pi k{\omega _c}/{\omega _N})} }{ {\pi k{\omega _c}/{\omega _N} } },{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = - M,…,0,…M\\
    &{w_0} = \frac{ { {\omega _c} } }{ { {\omega _N} } }
    \end{align}
    $$

  • 高通

    $$
    \begin{align}
    &{w_k} = -\frac{ { {\omega _c} } }{ { {\omega _N} } }\frac{ {\sin (\pi k{\omega _c}/{\omega _N})} }{ {\pi k{\omega _c}/{\omega _N} } },{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = - M,…,0,…M\\
    &{w_0} = 1-\frac{ { {\omega _c} } }{ { {\omega _N} } }
    \end{align}
    $$

    其中 ${\omega_c}$ 是 cutoff 频率 (角频率)。${\omega_N}$ 是 Nyquist 频率 (角频率)。

例如原序列是逐日的气温数据，时间步长是1天。做低通滤波，保留周期大于10天 ($f=\frac{1}{10}$) 的信号，那么

(1) 采样频率$sample=\frac{1}{1 day}=1$

(2) $\omega_{N}=0.5*sample *2\pi=\pi$ (Nyquist频率是构成序列的波的最大频率。想象至少三个点才能确定一个完整的波形，而三个点包含两个时间步长。也就是说一个波形对应的最小周期就是2个时间步长，那么频率是周期的倒数，一个波形对应的最大频率就是 $\omega_{N}$)

(3) $\omega_{c}=f*2\pi=\frac{1}{10day}*2\pi=\frac{\pi}{5}$ (角频率等于频率乘2$\pi$)
再例如原序列是逐小时的气温数据，时间步长是 1小时=$\frac{1}{24}$天。做高通滤波，保留周期小于30天 ($f=\frac{1}{30}$) 信号，那么

(1) 采样频率$sample=\frac{1}{1/24 day}=24$

(2) $\omega_{N}=0.5*sample *2\pi=24\pi $

(3) $\omega_{c}=f*2\pi=\frac{1}{30day}*2\pi=\frac{\pi}{15}$

带通滤波

带通滤波的权重公式为

$$
\begin{align}
&{w_k} = \frac{ { {\omega _2} } }{ { {\omega _N} } }\frac{ {\sin (\pi k{\omega _2}/{\omega _N})} }{ {\pi k{\omega _2}/{\omega _N} } } - \frac{ { {\omega _1} } }{ { {\omega _N} } }\frac{ {\sin (\pi k{\omega _1}/{\omega _N})} }{ {\pi k{\omega _1}/{\omega _N} } },{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = - M,…,0,…M\\
&{\omega _2} > {\omega _1}\\
&{w_0}=\frac{\omega _2 - \omega _1}{\omega _y}
\end{align}
$$

其中 $\omega_{0}$ 是通过 $k→0$ 取极限得到。使用带通滤波将保留角频率在 [$\omega_{1}, \omega_{2}$] 之间的信号。

响应函数

既然有了 $w_{k}$ 那么我们就可以通过公式 (1) 进行计算，得到滤波结果。那么为什么乘了这样的权重系数能达滤波的作用呢？

首先我们可以看一下滤波结果 $y_{n}$ 究竟是不是保留了我们想要的频率的信号。怎么看呢？就是用傅里叶变换把时域信号转换到频域上。即

$$
\begin{align}
Y(\omega ) = \sum\limits_{n = - M}^M { {y_n}{e^{ - i\omega n\Delta t} } }
\end{align}
$$

该公式同 傅里叶变换与滤波 中的公式 (14)。将公式 (1) 代入公式 (10)，得

$$
\begin{align}
Y(\omega ) &= \sum\limits_{n = - M}^M { {y_n}{e^{ - i\omega n\Delta t} } } \\
&= \sum\limits_{k = - M}^M { {w_k}{e^{ - i\omega k\Delta t} } } \sum\limits_{n = - M}^M { {x_{n - k} }{e^{ - i\omega (n - k)\Delta t} } } \\
&= W(\omega )X(\omega )
\end{align}
$$

可见 $y_{n}$ 的傅里叶变换等于 $w_{k}$ 和 $x_{n}$ 的傅里叶变换的乘积。也就是说新信号的频谱等于原信号的频谱乘权重系数的频谱。 如果 $W(\omega)$ 在 [$\omega_{1}, \omega_{2}$] 上等于0，在 [$\omega_{3}, \omega_{4}$] 等于1，那么与 $X(\omega)$ 相乘就会导致频谱在 [$\omega_{1}, \omega_{2}$] 上等于0，在 [$\omega_{3}, \omega_{4}$] 上保持不变。这就相当于 傅里叶变换与滤波 中所做的滤波一样，这不过在这里使用特定的函数，而 傅里叶变换与滤波 中人为手动地通过赋值改变频谱。

事实上公式 (3)(5)(7) 的频谱 $W(\omega)$ 就是能取得这种效果, 它也被称为响应函数。为了克服滤波前后造成的相位偏移，通常认为 $W(\omega)$ 是偶函数，即 $W(\omega)=W(-\omega)$ 。因此 $W(\omega)$ 的计算公式也写为()

$$
\begin{align}
W(\omega ) = {w_0} + 2\sum\limits_{k = 1}^M { {w_k}\cos (\pi k\omega /{\omega _N})}
\end{align}
$$

《Data Analysis Methods in Physical Oceanography, Third Edition》里的公式 (6.41) 少了系数2 ？下面通过举例来看看这个响应函数的曲线。

以低通滤波为例，条件如下：

原序列是逐小时的气温数据，时间步长是 1小时=$\frac{1}{24}$天。原信号由周期1,3,5,7天四个余弦波叠加，数据长度为3000，也就是3000/24=125天。通过低通滤波得到周期大于6天的信号(也就是得到周期7天的波)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 数组长度
N = 3000 

# 采样频率，步长是1小时=1/24天，所以频率是24
sample = 24 
omega_c = 1/6 * 2*np.pi # cutoff 角频率
omega_ny = 0.5*sample * 2*np.pi # Nyquist角频率

# 取权重点个数为 2M+1
M = 240 
k = np.arange(-M, M+1) # 波数

# 低通权重公式
wk = omega_c/omega_ny * np.sin(np.pi * k * omega_c/omega_ny) / (np.pi * k * omega_c/omega_ny)
w0 = omega_c/omega_ny
wk[k==0] = w0 # k==0的地方要重新赋值
k_plus = k[k>=1] # 考虑对称性，只取k为正数
wk_plus = wk[k>=1]
fft_x = fftfreq(N, 125/N) # 计算频率
omega = fft_x * 2 * np.pi # 转为角频率

# 通过离散傅里叶变换计算权重系数的频率Wk(响应函数)
term = 0
for i in range(k_plus.shape[0]):
    term = term + wk_plus[i] * np.cos(np.pi * k_plus[i] * omega / omega_ny)

Wk = w0 + 2*term


# 画图
fig, ax = plt.subplots()
ax.plot(fft_x, Wk)

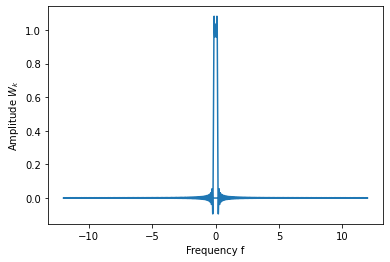
这就是低通滤波响应函数的图像。可以看到在高频部分 (f>1/7), $W_{k}=0$ 这样通过公式 (13) 将导致新序列在高频部分的频率为0，经过傅里叶逆变换之后，新序列的高频信号就被滤掉了，而只保留了低频部分 (因为 f<1/7的部分 $W_{k}=1$)。

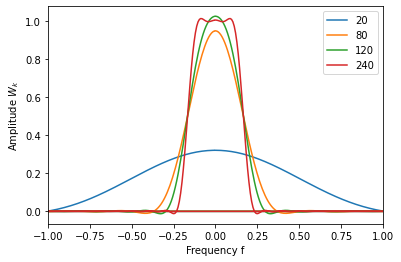
可以看到 $W_k$ 由1到0的转变很迅速，几乎是垂直的，这就意味着这种响应函数滤波滤得很干净。这与 M 的选取有关，M 越大滤波效果越好，但会造成更多的数据损失。 下面代码展现 M 的选取对响应函数的影响

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
def getWk(M):
    N = 3000 

    # 采样频率，步长是1小时=1/24天，所以频率是24
    sample = 24 
    omega_c = 1/6 * 2*np.pi # cutoff 角频率
    omega_ny = 0.5*sample * 2*np.pi # Nyquist角频率

    # 取权重点个数为 2M+1

    k = np.arange(-M, M+1) # 波数

    # 低通权重公式
    wk = omega_c/omega_ny * np.sin(np.pi * k * omega_c/omega_ny) / (np.pi * k * omega_c/omega_ny)
    w0 = omega_c/omega_ny
    wk[k==0] = w0 # k==0的地方要重新赋值
    k_plus = k[k>=1] # 考虑对称性，只取k为正数
    wk_plus = wk[k>=1]
    fft_x = fftfreq(N, 125/N) # 计算频率
    omega = fft_x * 2 * np.pi # 转为角频率

    # 通过离散傅里叶变换计算权重系数的频率Wk(响应函数)
    term = 0
    for i in range(k_plus.shape[0]):
        term = term + wk_plus[i] * np.cos(np.pi * k_plus[i] * omega / omega_ny)

    Wk = w0 + 2*term
    return Wk

Wlist = []
label = []
for M in [20,80,120,240]:
    Wlist.append(getWk(M))
    label.append(str(M))
# 画图
fig, ax = plt.subplots()
for i in range(len(Wlist)):
    ax.plot(fft_x, Wlist[i], label=label[i])
ax.set_xlim([-1,1]) # x 轴范围缩小到 [-1, 1]
ax.set_xlabel('Frequency f')
ax.set_ylabel('Amplitude $W_{k}$')
ax.legend()

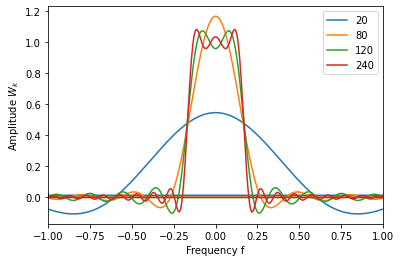
图中为 M=20,80,120,240 的情况下 $W_k$ 的曲线，是对 $f=[-1,1]$ 的局部放大。很明显 M 越大， $W_k$ 的最大值维持在1， 最小值维持在0，且0,1之间的转变迅速 (斜率大)。因此在对不同数据进行滤波时，应该选取合适的 M， 看一下 $W_k$ 是否合理。从滤波效果来说，M 越大越好

 

那么具体的滤波手段有两种，一种是通过公式 (1) 原信号直接乘权重系数。另一种是通过公式 (13) ，原信号先转为频域，乘响应函数，最后傅里叶逆变换转为时域。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq,fftshift, ifft

# 数组长度
N = 3000 

# 原序列 
n = np.arange(0, 125, 1/24) 
x = np.cos(2*np.pi * 1/1 * n) + np.cos(2*np.pi * 1/3 * n) + np.cos(2*np.pi * 1/5 * n) + np.cos(2*np.pi * 1/7 * n)

# 采样频率，步长是1小时=1/24天，所以频率是24
sample = 24 
omega_c = 1/6 * 2*np.pi # cutoff 角频率
omega_ny = 0.5*sample * 2*np.pi # Nyquist角频率

# 取权重点个数为 2M+1
M = 240 
k = np.arange(-M, M+1) # 波数

# 低通权重公式
wk = omega_c/omega_ny * np.sin(np.pi * k * omega_c/omega_ny) / (np.pi * k * omega_c/omega_ny)
w0 = omega_c/omega_ny
wk[k==0] = w0 # k==0的地方要重新赋值
k_plus = k[k>=1] # 考虑对称性，只取k为正数
wk_plus = wk[k>=1]
fft_x = fftfreq(N, 125/N) # 计算频率
omega = fft_x * 2 * np.pi # 转为角频率

# 通过离散傅里叶变换计算权重系数的频率Wk(响应函数)
term = 0
for i in range(k_plus.shape[0]):
    term = term + wk_plus[i] * np.cos(np.pi * k_plus[i] * omega / omega_ny)

Wk = w0 + 2*term

# 直接乘权重系数
y2 = np.zeros((N))
for t in range(M, N-M):
    for j in range(k.shape[0]):
        y2[t] = y2[t] + wk[j] * x[t-k[j]]


# 画图
fig, ax = plt.subplots()
ax.plot(fft_x, Wk)

X = fft(x)  
Y = X * Wk
y = ifft(Y)
fig, ax = plt.subplots(1,2,figsize=(15,4))
ax[0].plot(n, y, label='$W_{\omega}X(\omega)$')
ax[0].plot(n,  np.cos(2*np.pi * 1/7 * n), label='$cos(2\pi*\\frac{1}{7})$')
ax[0].plot(n,  y2, label='$w_{k}x_{n-k}$')
ax[0].legend()

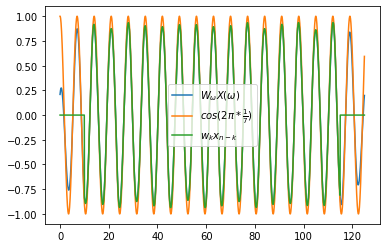
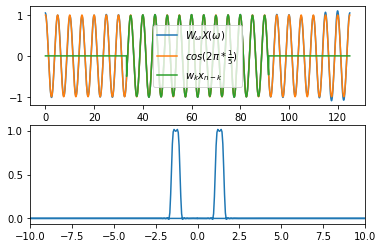
蓝线是频谱相乘再傅里叶变换的结果，橙线是周期为7天的波，绿线是直接乘权重系数的结果。可以看出三根线都较为接近，说明滤波起到了很好的效果。此外，蓝线并没有损失数据，而绿线损失了数据。 因此可以通过傅里叶变换的方法避免数据的损失，从图中可以看出这种方法保留下的两端的数据仍具有较好的准确性。图中绿线在两端各损失了 $M=240$ 个点，共480个点。从图中看出蓝线和绿线的最大值都小于1，也就是说滤波后振幅减弱了，这主要是因为 M 的值不够大。

Lanczos Window

以上的滤波操作还不能被称为 Lanczos 滤波。Lanczos滤波需要对以上的权重函数再乘一个因子 $\sigma$ 。其公式为

$$
\begin{align}
\sigma (M,k) = \frac{ {\sin (\pi k/M)} }{ {\pi k/M} }
\end{align}
$$

于是公式 (3)(5)(7) 变成

$$
\begin{align}
&低通{w_k} = \frac{ { {\omega _c} } }{ { {\omega _N} } }\frac{ {\sin (\pi k{\omega _c}/{\omega _N})} }{ {\pi k{\omega _c}/{\omega _N} } }\sigma(M,k){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}\\
&高通{w_k} = -\frac{ { {\omega _c} } }{ { {\omega _N} } }\frac{ {\sin (\pi k{\omega _c}/{\omega _N})} }{ {\pi k{\omega _c}/{\omega _N} } }\sigma(M,k){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}\\
&带通{w_k} = (\frac{ { {\omega _2} } }{ { {\omega _N} } }\frac{ {\sin (\pi k{\omega _2}/{\omega _N})} }{ {\pi k{\omega _2}/{\omega _N} } } - \frac{ { {\omega _1} } }{ { {\omega _N} } }\frac{ {\sin (\pi k{\omega _1}/{\omega _N})} }{ {\pi k{\omega _1}/{\omega _N} } })\sigma(M,k){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}
\end{align}
$$

$\sigma$ 因子的作用是加快响应函数从在0,1之间的转变，并且减弱 Gibbs 现象。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
def getWk(M):
    N = 3000 

    # 采样频率，步长是1小时=1/24天，所以频率是24
    sample = 24 
    omega_c = 1/6 * 2*np.pi # cutoff 角频率
    omega_ny = 0.5*sample * 2*np.pi # Nyquist角频率

    # 取权重点个数为 2M+1

    k = np.arange(-M, M+1) # 波数

    # 低通权重公式
    wk = omega_c/omega_ny * np.sin(np.pi * k * omega_c/omega_ny) / (np.pi * k * omega_c/omega_ny)
    w0 = omega_c/omega_ny
    wk[k==0] = w0 # k==0的地方要重新赋值
    k_plus = k[k>=1] # 考虑对称性，只取k为正数
    wk_plus = wk[k>=1]
    fft_x = fftfreq(N, 125/N) # 计算频率
    omega = fft_x * 2 * np.pi # 转为角频率

    sigma = np.sin(np.pi * k_plus / M) / (np.pi * k_plus / M)

    wk_plus = wk_plus * sigma
    # 通过离散傅里叶变换计算权重系数的频率Wk(响应函数)
    term = 0
    for i in range(k_plus.shape[0]):
        term = term + wk_plus[i] * np.cos(np.pi * k_plus[i] * omega / omega_ny)

    Wk = w0 + 2*term
    return Wk

Wlist = []
label = []
for M in [20,80,120,240]:
    Wlist.append(getWk(M))
    label.append(str(M))
# 画图
fig, ax = plt.subplots()
for i in range(len(Wlist)):
    ax.plot(fft_x, Wlist[i], label=label[i])
ax.set_xlim([-1,1]) # x 轴范围缩小到 [-1, 1]
ax.set_xlabel('Frequency f')
ax.set_ylabel('Amplitude $W_{k}$')
ax.legend()

Gibbs 现象就是在0,1,转换出曲线强烈振荡的现象，与前天相比较。加入了 $\sigma$ 因子很好地减弱了 Gibbs 现象。

总结

下面把Lanczos代码做一下汇总总结

首先定义一个生成响应函数 $W(\omega)$ 和 权重系数 $w_k$ 的函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
def lanczos(N, sample, M, _f, _tp):
    '''

    Parameters
    ----------
    N : int
        数据长度.
    sample : float
        采样频率.
    M : int
        权重点数，总权重数为2M+1个.
    _f : float or list
        cutoff频率。低通和高通为一个数，带通为列表，长度为2，由小到大.
    _tp : TYPE
        滤波类型。 低通:'low' ; 高通: 'high' ; 带通: 'band'

    Returns
    -------
    W : array
        响应函数.
    wk : array
        权重系数

    '''   
    # cutoff频率
    if (_tp=='low')| (_tp=='high'):
        omega_c = _f * (2 * np.pi)

    if _tp=='band':
        omega1 = _f[0] * 2 * np.pi
        omega2 = _f[1] * 2 * np.

    # Nyquist频率
    omega_ny = sample*0.5 * 2 * np.pi

    k = np.arange(-M,M+1)

    # 计算权重系数
    if _tp=='low':
        wk = omega_c/omega_ny * np.sin(np.pi * k * omega_c/omega_ny) / (np.pi * k * omega_c/omega_ny)
        w0 = omega_c/omega_ny
    if _tp=='high':
        wk = -omega_c/omega_ny * np.sin(np.pi * k * omega_c/omega_ny) / (np.pi * k * omega_c/omega_ny)
        w0 = 1 - omega_c/omega_ny
    if _tp=='band':
        wk = omega2/omega_ny * np.sin(np.pi * k * omega2 / omega_ny) / (np.pi * k * omega2/omega_ny) - \
        omega1/omega_ny * np.sin(np.pi * k * omega1 / omega_ny) / (np.pi * k * omega1/omega_ny)
        w0 = (omega2 - omega1)/omega_ny

    wk[k==0] = w0
    k_plus = k[k>=1]
    wk_plus = wk[k>=1]


    fft_x=fftfreq(N,T/N) 
    omega = fft_x * 2 * np.pi

    # 计算sigma因子
    sigma = np.sin(np.pi * k / M) / (np.pi * k / M)
    sigma_plus = np.sin(np.pi * k_plus / M) / (np.pi * k_plus / M)

    # 系数乘sigma因子
    wk = wk * sigma 
    wk_plus = wk_plus * sigma_plus

    # 计算响应函数
    term = 0
    for i in range(k_plus.shape[0]):
        term = term + wk_plus[i] * np.cos(np.pi * k_plus[i] * omega / omega_ny)

    W = w0 + 2*term

    return W, wk

然后可以分别利用响应函数 $W(\omega)$ 和权重系数 $w_k$ 进行滤波

  • 低通 (高通)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq,fftshift, ifft 

N = 3000
T = 125
M = 800
k = np.arange(-M,M+1)

fft_x = fftfreq(N, T/N) 
omega = fft_x * 2 * np.pi

# 原序列 
n = np.arange(0, 125, 1/24) 
x = np.cos(2*np.pi * 1/1 * n) + np.cos(2*np.pi * 1/3 * n) + np.cos(2*np.pi * 1/5 * n) + np.cos(2*np.pi * 1/7 * n)


WL, wkL = lanczos(N=N, T=T, M=M, _f=1/6, _tp='low')

# 利用响应函数做傅里叶逆变换
X = fft(x)  
Y = X * WL
yW = ifft(Y)


# 直接乘权重系数
yw = np.zeros((N))
for t in range(M, N-M):
    for j in range(k.shape[0]):
        yw[t] = yw[t] + wkL[j] * x[t-k[j]]


fig, ax = plt.subplots(2,1,)
ax[0].plot(n, yW, label='$W_{\omega}X(\omega)$')
ax[0].plot(n, np.cos(2*np.pi * 1/7 * n), label='$cos(2\pi*\\frac{1}{7})$')
ax[0].plot(n, yw, label='$w_{k}x_{n-k}$')
ax[0].legend()

ax[1].plot(omega, WL)
ax[1].set_xlim([-10,10])

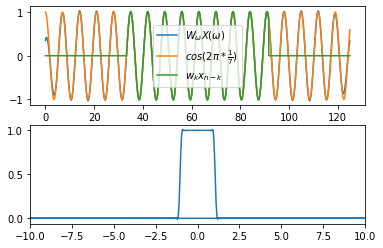
图2 是响应函数 $W(\omega)$ 的图像，对比图1 来看这样的响应函数能够很好地完成滤波。在以上代码中将 M 提高到了 800，如果 M=240 则 滤波效果并不很好。所以在滤波之前一定要对比参考响应函数 $W(\omega)$

以上代码是低通滤波 (高通滤波同理)。此外还可以做带通滤波

  • 带通
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
N = 3000
T = 125
M = 800
k = np.arange(-M,M+1)


fft_x = fftfreq(N, T/N) 
omega = fft_x * 2 * np.pi

# 原序列 
n = np.arange(0, 125, 1/24) 
x = np.cos(2*np.pi * 1/1 * n) + np.cos(2*np.pi * 1/3 * n) + np.cos(2*np.pi * 1/5 * n) + np.cos(2*np.pi * 1/7 * n)


WL, wkL = lanczos(N=N, T=T, M=M, _f=[1/6, 1/4], _tp='band')


# 利用响应函数做傅里叶逆变换
X = fft(x)  
Y = X * WL
yW = ifft(Y)


# 直接乘权重系数
yw = np.zeros((N))
for t in range(M, N-M):
    for j in range(k.shape[0]):
        yw[t] = yw[t] + wkL[j] * x[t-k[j]]


fig, ax = plt.subplots(2,1,)
ax[0].plot(n, yW, label='$W_{\omega}X(\omega)$')
ax[0].plot(n, np.cos(2*np.pi * 1/5 * n), label='$cos(2\pi*\\frac{1}{5})$')
ax[0].plot(n, yw, label='$w_{k}x_{n-k}$')
ax[0].legend()

ax[1].plot(omega, WL)
ax[1].set_xlim([-10,10])