傅里叶变换与滤波

前言

在读了王老师的那篇探讨行星波影响冬季风关系的文章后。我也想自己动手计算一下EP通量。论文的计算步骤里有一步是要将各变量进行傅里叶分解，保留1-3波。由于当时不了解傅里叶变换，这一步也就跳过去了。算出来的EP通量始终小了一个量级。我想也许就是因为没做滤波导致的？不管是不是这个原因，我还是决定学习一下傅里叶变换。目前没怎么翻书，看了两篇知乎文章，感觉大致就懂了。

傅里叶变换 (scipy.fft)

如何理解傅里叶变换公式？

如何通俗地解释什么是离散傅里叶变换？

---

连续傅里叶变换

傅里叶变换的基本思想就是

任何连续信号(周期性或非周期性的)都可以由一组适当的正弦曲线组合而成

假设时间为 $x$ ，每个时间点对应的信号振幅为 $y(x)$。傅里叶级数有如下公式：

$$
\begin{equation}
y(x) = \frac{ { {a_0} } } {2} + \sum\limits_{n = 1}^N { {a_n} } \cos (2\pi fnx) + {b_n}\sin (2\pi fnx)
\end{equation}
$$

这里规定了离散的频率 $2\pi fn$ 。因为这样的形式组成了一组正交基，满足以下等式

$$
\begin{equation}
\int_{ {\rm{ - } }\frac{T}{2} }^{\frac{T}{2} } {\cos (mx)\cos (nx)dx} = 0 (m \ne n)
\end{equation}
$$

这里在-T/2,T/2之间积分是假定变换的对象 $y(x)$ 是周期函数，即在一个周期内积分为0(上式cos换成sin也成立)。而对于非周期函数，同样可以使用上式，因为非周期函数就是令 $T \to \infty $ 。

基于正交特性，便可以求出 $a_n$ 和 $b_n$

$$
\begin{align}
{a_n} = \frac{2}{T}\int_{ {x_0} }^{ {x_0} + T} {y(x)\cos (2\pi fnx)dx} \\
{b_n} = \frac{2}{T}\int_{ {x_0} }^{ {x_0} + T} {y(x)\sin (2\pi fnx)dx}
\end{align}
$$

$x_0$ 是任意值，因为我们只需要在一个周期 $T$ 内积分就可以。

---

离散傅里叶变换

通常我们需要处理的信号并非严格周期更不是连续的，例如逐年气温序列。假设序列的长度是 $N$ ，我们只需要将积分符号换成求和符号，将 $T$ 换成 $N$，从 $n=0$ 求和到 $n=N$ 即可。我们利用欧拉公式 $ e^{ix} = \cos x + i\sin x $ 重写 $a_n, b_n$ 的表达式

$$
\begin{align}
y(x) &= \frac{ { {a_0} } }{2} + \sum\limits_{n = 1}^N { {a_n}\cos (2\pi fnx) + {b_n}\sin (2fnx) } \\
&= \sum\limits_{ - N}^N { {c_n} } \cdot (\cos (2\pi fnx) + i\sin (2\pi fnx)) \\
&= \sum\limits_{ - N}^N { {c_n} } \cdot {e^{i2\pi fnx} }
\end{align}
$$

这是复频域傅里叶级数，也是快速傅里叶变换计算的原理。通过复频域表示时，会出现虚数单位，而这个是我们在三角级数表现方式中不曾出现的，而最后负频域表示方式要能够化成和三角级数的相等的表达形式，所以必须想办法消掉虚数单位。所以我们就想到共轭复数 $e^{-ix}=cosx-isinx$ 。有了共轭复数，我们可以通过两个互为共轭的复数加法将虚数消掉。将频域$1-N$求和转化为复频域$-N—N$求和。

$c_n$可用待定系数的方式求解，即设

$$
\begin{align}
{c_n} = \left \lbrace \begin{array} {l}
p + iq{\kern 1pt} {\kern 1pt} {\kern 1pt} (n > 0)\\
p - iq{\kern 1pt} {\kern 1pt} {\kern 1pt} (n < 0)
\end{array} \right.
\end{align}
$$

可求得 $c_n$ 与 $a_n , b_n$ 的关系

$$
\begin{align}
{c_n} = \left \lbrace \begin{array} {l}
\frac{1}{2}({a_n} - i{b_n}){\kern 1pt} {\kern 1pt} {\kern 1pt} (n > 0)\\
\frac{1}{2}{a_0}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (n = 0)\\
\frac{1}{2}({a_n} + i{b_n}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (n < 0)
\end{array} \right.
\end{align}
$$

将公式(3)(4)中的 $T$ 换为 $N$ (非周期函数假定周期无穷大，而信号的长度为 $N$ 。$x$ 换为 $n$ (第n个信号点)。$n$ 换为 $k$ ($N$ 个采样内振动 $k$ 个周期，相当于波数)。积分号换为求和号，则 $a_n , b_n$ 的离散形式为

$$
\begin{align}
{a_k} = \frac{2}{N}\sum\limits_{n = 0}^{N - 1} {y(n)\cos (\frac{ {2\pi k} }{N}n)} \\
{b_k} = \frac{2}{N}\sum\limits_{n = 0}^{N - 1} {y(n)\sin (\frac{ {2\pi k} }{N}n)}
\end{align}
$$

代入公式 (9) 得 $c_n$ 的离散形式

$$
\begin{align}
c(k) &= \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {y(n)} (\cos (\frac{ {2\pi k} }{N}n) - i\sin (\frac{ {2\pi k} }{N}n))\\
&= \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {y(n)} \cdot {e^{ - i\frac{ {2\pi k} }{N}n} }
\end{align}
$$

这里可能只考虑 $n>0$ 的情况，因为不存在 $y(-n)$ 的值。此外，在Scipy.fft.fft 中计算的 $c(k)$ 没有常数 $\frac{1}{N}$ 。而将 $\frac{1}{N}$ 移到傅里叶逆变换中。 Scipy.fft.fft 给出的计算公式为

# 前面没乘 1/n
c[k] = np.sum(x * np.exp(-2j * np.pi * k * np.arange(n)/n))

 

• 如何理解 $k,N,f$ 的关系？

  $N$ 在公式中是信号采样点的个数，数据的长度。在假定周期无限大的情况下，整个数据的长度 $N$ 就是整个原信号周期 $T$ 。在公式 (12)的 $cos(\frac{2\pi k}{N}n)$ 中每个 $k$ 代表一个波，而 $n$ 的作用是对这个波进行采样 (相当于x轴坐标)。公式 (13) 中每个波 $e^{ - i\frac{ {2\pi k} }{N}n}$ 与原信号进行内积(对应位置相乘并求和) 。由内积的特性，如果波与原数据越接近，则内积结果越大 (例如5x5>4x6)。傅里叶变化公式 (13) 的另一种理解就是找到各个 $k$ 对应的波与原数据的内积，内积越大说明该波贡献也越大，$c_n$ 就越大。

  我们说 $N$ 是原信号的周期，然而傅里叶变化找出的各个波的周期并不是 $N$ 而是 $\frac{N}{k}$ ($2\pi /(\frac{2\pi k}{N})$)。想象一下，如果原数据的采样点有 $N=40$ 。在这个范围内，一个波产生了 5 个完整波形，那么这个波的周期就是 $40/5=8$ , 即 $k=5$ 。5个完整波形意味着波数就是5，那么 $k$ 就是波数。 公式(1) - (4) 中的 $f$ 为原信号的频率，$N$ 的倒数。而傅里叶变化的各个小波的频率为 $\frac{k}{N}$ 。

---

 

傅里叶逆变换

仔细观察可以发现公式 (7) 的自变量是时间 $x$ 。因此显示的是信号的时域特征。而公式 (13) 的自变量是波数 $k$ 或者说频率 $\frac{k}{N}$ ，因此它显示的是信号的频域特征。我们用公式 (13) 将信号 $y(x) $ 转到频域上，就是傅里叶变换。用公式 (7) 把信号 $c_n$ 转回时域上就是傅里叶逆变换。公式 (7) 写得并不是与 公式 (13) 很对应，因此我们重写一下公式 (7) 和 (13)

$$
\begin{align}
c(k) &= \sum\limits_{n = 0}^{N - 1} {y(n) \cdot {e^{ - i\frac{ {2\pi k} }{N}n} } } \\
y(n) &= \frac{1}{N}\sum\limits_{n = 0}^{N - 1} { {c_k} \cdot {e^{i\frac{ {2\pi k} }{N}n} } }
\end{align}
$$

公式 (14) 和 (15) 分别就是傅里叶变换和傅里叶逆变换。这里为了与Scipy.fft.fft 的算法一致，将本该在公式 (14) 中的 $\frac{1}{N}$ 放在了公式 (15) 中。

---

Scipy.fft

fft 傅里叶变换

Python 科学计算库 Scipy 提供了方便快捷的傅里叶变换函数。使用这个函数需要注意一些细节。

首先我们人造一组信号用于测试.

# 这是由两个角频率为 10 和 15 的信号叠加的。注意是“角频率”
# 其频率分别为10/(2π)=1.59 和 15/(2π)=2.39
def f(n):
    return np.cos(10*n) + np.cos(15*n)

我们将时间0~7划分为1000份

import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq,fftshift, ifft
import numpy as np

# 数据长度
N = 1000

# 时间长度，单位暂定为秒
T = 7

# 生成采样点和信号
x = np.linspace(0,T,N)
y = f(x)

# 进行傅里叶变换
fft_y = fft(y)  

生成的 fft_y 即为公式 (14) 中的 $c_k$。在公式 (14) 中 $k=0,1,2,3···N-1$。 想象一下，$k$ 表征波数，如果 $k>\frac{N}{2}$ ，那么意味着这个波每个周期占了不到两个采样点，而波至少需要两个采样点才能确定一个周期波形 (Nyquist 频率概念)。所以 Scipy 采用一种 $-k$ 的方式计算。已知原信号周期为 $N$ ，$k=0,1,2,3···\frac{N}{2}$ 都没什么问题，而考虑周期性的话 $ c(\frac{N}{2}+1 )= c((\frac{N}{2}+1)-N)=c(-\frac{N}{2}+1)$ , 这样 $k$ 被转到了负数上，而由于周期性，计算得到的数值不会改变。例如当 $N=8$ 时，$k=[0, 1, 2, 3, 4, 5, 6, 7]$ 变为 $k=[0, 1, 2, 3, -4, -3, -2, -1]$

下面对比一下使用 fft 和不使用它的区别

# 利用 scipy.fft.fft 函数计算
fft_y=fft(y)

# 生成 k， 但实际上生成的是 k/T
fft_x = fftfreq(N,T/N) 

# [0, 1, 2, 3, -4, -3, -2, -1] 排序调整为
# [-4, -3, -2, -1, 0, 1, 2, 3]
fftshift_x = fftshift(fft_x)
fftshift_y = fftshift(fft_y)

# 利用公式计算
k = np.arange(0,N)
yy = []
for i in range(N):
    yy.append(np.sum(f(x) * np.exp(-2j * np.pi * k[i] * np.arange(N)/N)))
yy = np.array(yy)

# 画图
fig, ax = plt.subplots(1,2,figsize=(15,4))
ax[0].plot(fftshift_x, abs(fftshift_y))
ax[0].set_title('函数计算',fontfamily='SimSun')
ax[1].plot(k/T, abs(yy))
ax[1].set_title('公式计算',fontfamily='SimSun')

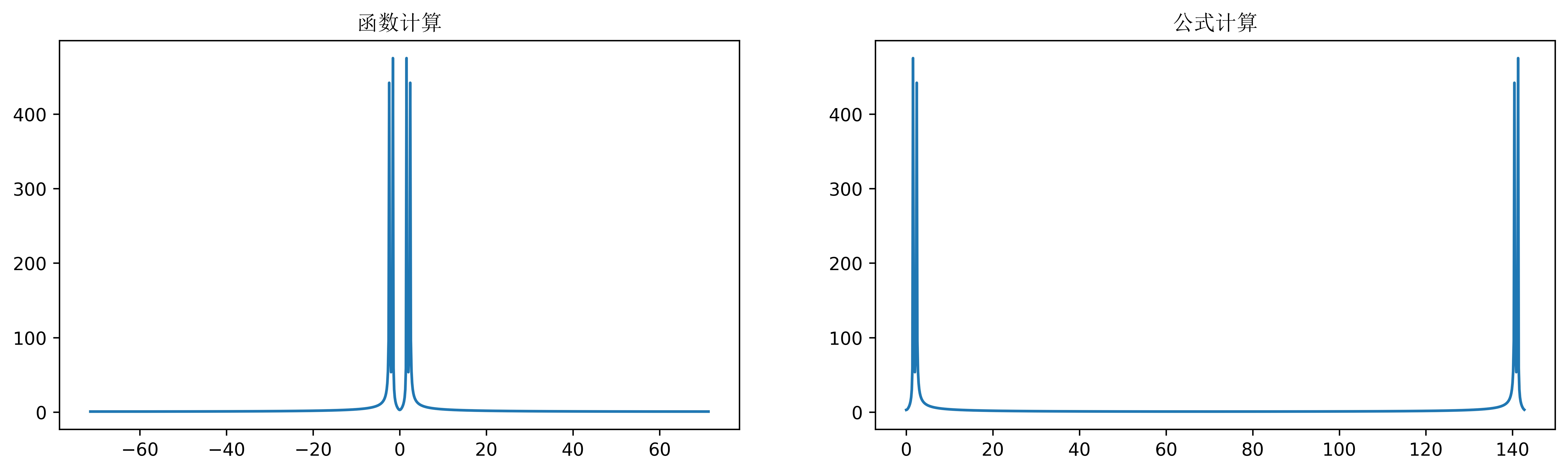
可以看到两种方法计算出的峰值是一样的，只是在x轴是有所不同。图像给出的x轴对应的就是各个波分量的频率。这样看来还是左图更为合理一些，因为 Nyquist 频率的概念存在，波的频率不应该超过 $\frac{N}{2}/T=1000/2/7≈71$

• 注意事项

  第5行中生成的 fft_x 并不是$k$ 而是 $\frac{k}{T}=\frac{k}{7}$ 也就是真正的这个波分量的频率。我们在公式 (14) 中看到的波频率不应该是 $\frac{k}{N}=\frac{k}{1000}$ 吗？因为在编程过程中 $N$ 只是数据的长度，它不具有单位。在公式 (14) 中 $N$ 也是数据的长度，但它实际上是 $\scriptstyle N=N \times d=N \times 1$ 。$d$ 是采样频率，比如我们有1981-2020年的逐日数据，那么$N=40 \times 365,d=1day$。或者 $d=\frac{1}{30}month$ 。因此 fft_x 代表的频率其实是 $\frac{k} {T}=\frac{k} {N \times d}=\frac{k} {1000 \times 7/1000}$

  不论是哪种方法傅里叶变换总是要输出两个量 $a_n$ 和 $b_n$ 。在复频域中则对应实部和虚部 (注意实部与 $a_n$ 可以相差0.5或$N$ 等常数倍数)。第21行和23行使用的是 abs 表示对复数取模，即根号下实部的平方加虚部的平方。我认为这种处理是比较合理的，因为实部和虚部同样重要，应该综合考虑其分量的振幅。如果不取模直接用 matplotlib ，则只会画出实部。

ifft 傅里叶逆变换与滤波

从频域图像中可以看出，频率主要有两个峰值 (四个峰值，其中两个是周期性导致的，看一半即可)。用 np.argsort() 获取排序索引找到峰值对应的频率

# index[0]与index[1]对应两个相等的最高峰值，相等指的是模相等。其实际数值互为共轭
# 即实部相等，虚部相反。index[2],index[3] 为两个次高的峰值
index = np.argsort(abs(fftshift_y))[::-1][0:4]

# 找到峰值对应的频率
print(fftshift_x[index])

# output: array([-1.57142857,  1.57142857, -2.42857143,  2.42857143])

可以计算一下我们一开始是用角频率为10和15的两个信号叠加的。频率等于角频率除以 2π 所以10/(2π) = 1.59和15/(2π) = 2.39 。这与程序输出结果一致。我们准确的找出了信号中的两个主频率。

利用这一点，我们就可以实现滤波。例如我想去除掉 $cos(15\pi x)$ 这个波。那么我只需要将图像中的那个次高峰变为0即可。因为次高峰对应的频率2.39，也就是角频率15。那么我们只需要

fftshift_y[index[[2,3]]] = 0

好了，现在频域上我们已经去掉了角频率为15的波，现在需要把频域信号转回时域上。也就是傅里叶逆变换。基本公式也就是公式 (15)。我们将处理好的 $c_n$ 代入公式 (15) 计算出 $y(x)$ 也就完成了逆变换。

在 Scipy.fft.ifft 可以帮助我们快速实现这一点。需要注意的是 ifft 的输入量只能是 fft 和 fftfreq 的直接输出量，不能是用 fftshift 调整顺序之后的量。

# 傅里叶逆变换
ifft_y = ifft(fft_y)

fig2, ax2 = plt.subplots(1,2,figsize=(15,4))
ax2[0].plot(x, ifft_y, label='ifft')
ax2[0].plot(x, np.cos(10*n), label='cos(10x)')
ax2[0].legend()

# 对滤波后的信号再做一次傅里叶变换，检测滤波效果
ax2[1].plot(fft_x, fft(ifft_y), label='ifft again')
ax2[1].legend()

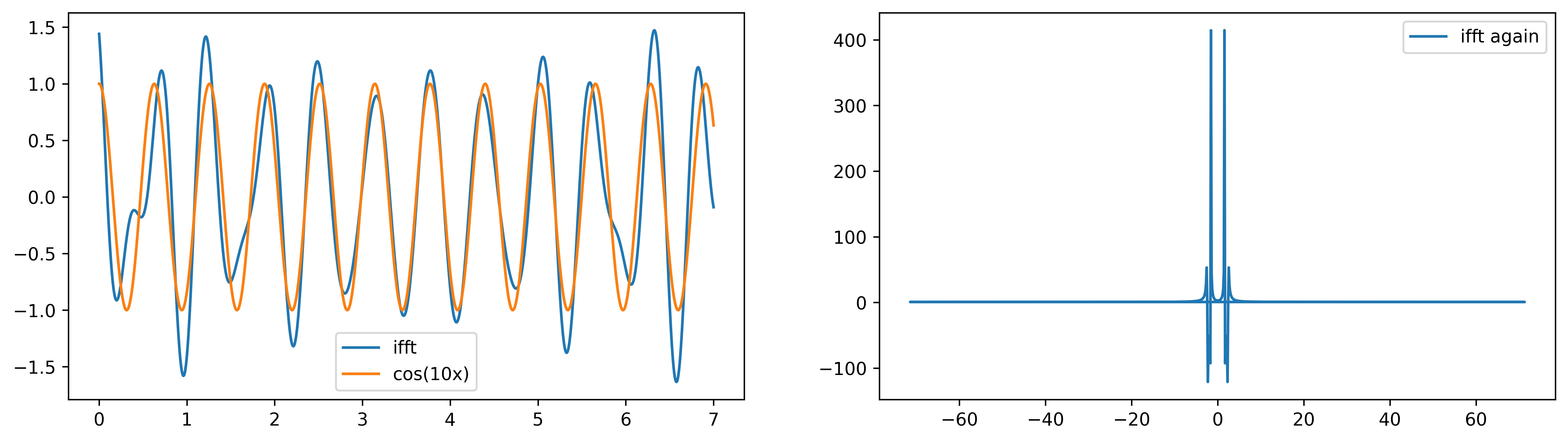
可以看到第一张图，滤波后的曲线与 $cos(10x)$ 的曲线比较接近，几乎没有受到 $cos(15x)$ 的影响，但并不是完全重合。对滤波后的时域信号再做一次傅里叶变换，可以看到峰值只剩一个主峰。但在0附近仍存在一个小峰没有去除掉。这个信号的来源不是很清楚，与离散傅里叶变换的误差有关？